Teorema de la Divergencia de Gauss
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem relating the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is.
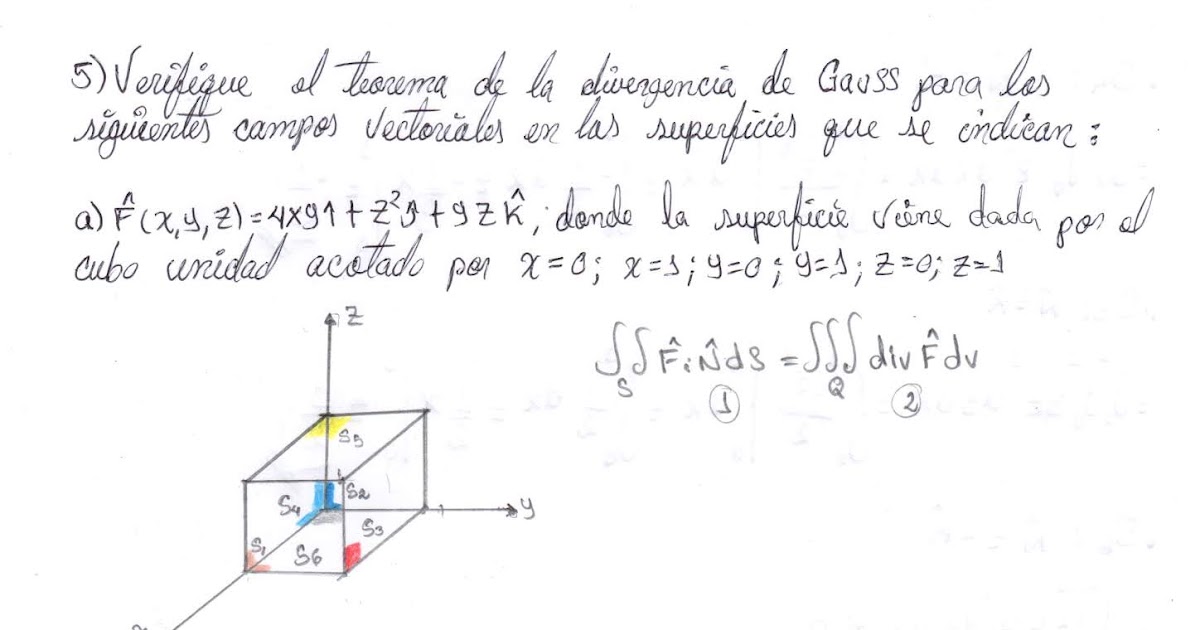
Teorema de la Divergencia de Gauss. EJERCICIO DE FINAL DE UNIVERSIDAD . Cálculo en Varias

Entonces. ∭Ediv ⇀ FdV = ∬S ⇀ F ⋅ d ⇀ S. Figura 16.8.1: El teorema de divergencia relaciona una integral de flujo S a través de una superficie cerrada con una triple integral sobre un sólido E encerrado por la superficie. Recordemos que la forma de flujo del teorema de Green afirma que. ∬Ddiv ⇀ FdA = ∫C ⇀ F ⋅ ⇀ NdS.
Teorema de la Divergencia de Gauss Sea 𝔷 una regiÛn solida limitada por una superficie 𝕆, y

El teorema de la divergencia se ha utilizado para desarrollar varias ecuaciones en el estudio del flujo de fluidos; por ejemplo, la ecuación de Euler y la ecuación de Bernoulli . La ecuación de Euler relaciona la velocidad, la presión y la densidad de un campo en movimiento, mientras que la ecuación de Bernoulli describe la sustentación.
TEOREMA DE GAUSS SOBRE LA DIVERGENCIA YouTube

Introducción El teorema de Gauss, también conocido como "Teorema de la divergencia", es aquel relaciona una integral triple sobre un volúmen \(W\) con una integral de superficie sobre su frontera, la cual es llamada \(\partial{W}\). Para aprender a aplicar el teorema de Gauss debemos tener en cuenta dos conceptos. Primero, tenemos que saber orientar la superficie \(\partial{W}\) que.
Teorema de la Divergencia de Gauss [CVV / 2021.01] YouTube

En esta sección utilizaremos el teorema de divergencia para encontrar una fórmula para la solución de la ecuación de Poisson. \vecs { \nabla} ^2\varphi = 4\pi\rho \nonumber. Aquí \rho=\rho (\vecs {r} ) hay una función dada (continua) y \varphi es la función desconocida que deseamos encontrar.
Teorema de Divergencia de Gauss

n ^. . es una función cuya salida son vectores unitarios normales en la superficie de S. . . Esto es lo que afirma el teorema de la divergencia: é ∭ V div F d V ⏟ Suma los pedacitos de flujo hacia afuera de V = ∬ S F ⋅ n ^ d Σ ⏞ Integral de flujo ⏟ Mide todo el flujo hacia afuera a través de la frontera de V.
TEMA TEOREMA DIVERGÊNCIA DE GAUSS YouTube

Suscribete a mi Canal: http://bit.ly/ULHegl - MI Profesor de Matemáticas - Calcular el flujo del campo F(x,y,z)=(xy^2,yz,zx^2 ) a traves de la frontera del.
Teorema de Gauss o de la divergencia. Ejemplo 3 YouTube

Cálculo de Varias Variables: https://www.youtube.com/playlist?list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9ACalcular la integral de superficie, empleando el teorema.
Aula UE Cómo funciona el Teorema de la divergencia YouTube

En cálculo vectorial, el teorema de la divergencia, también conocido como teorema de Gauss o teorema de Gauss-Ostrogradski, es un teorema que relaciona el flujo de un campo vectorial a través de una superficie cerrada con la divergencia del campo en el volumen delimitado por dicha superficie. De forma más precisa, el teorema de la.
Ejemplo Teorema de Gauss (de la divergencia) YouTube

El teorema de la divergencia, también conocido como teorema de Gauss, es una herramienta fundamental en el cálculo vectorial. Este teorema establece una relación entre una integral de superficie cerrada y una integral de volumen, permitiendo calcular el flujo de un campo vectorial a través de una superficie cerrada en función de las.
FUNCIONES VECTORIALES Teorema De La Divergencia o teorema de Gauss
Transcripción del video. vamos ahora a demostrar el teorema de la divergencia que nos dice que el flujo el flujo a través de una superficie es de algún campo vectorial que vamos a llamarle efe efecom con flechita porque es un campo vectorial este flujo que lo podemos expresar como la integral doble a lo largo de esta superficie de efe punto.
Teorema De La Divergencia De Gauss Un Ejemplo En Coordenadas Cilindricas Otosection

En cálculo vectorial, el teorema de la divergencia, también conocido como teorema de Gauss o teorema de Ostrogradsky, es un teorema que relaciona el flujo de un campo vectorial a través de una superficie cerrada con la divergencia del campo en el volumen encerrado. Más precisamente, el teorema de la divergencia establece que la integral de.
Teorema de Gauss o de la divergencia. Ejemplo 2 (directamente) YouTube

La Ley de Gauss en términos de divergencia puede escribirse como: ∇ ⋅ E = ρ ϵ0 (Local version of Gauss' Law) (17.4.1) (17.4.1) ∇ ⋅ E → = ρ ϵ 0 (Local version of Gauss' Law) donde ρ ρ está la carga por unidad de volumen en una posición específica en el espacio. Esta es la versión de la Ley de Gauss que suele verse en los.
Teorema de la Divergencia de Gauss Gauss's Divergence Theorem Video 168 YouTube

El teorema de la divergencia. Supongamos que S es una superficie cerrada, lisa y a trozos que encierra el sólido E en el espacio. Supongamos que S está orientado hacia el exterior, y que F es un campo vectorial con derivadas parciales continuas en una región abierta que contiene a E (Figura 6.87).Entonces
PPT Teorema Divergensi Gauss PowerPoint Presentation, free download ID2431126

es algún volumen de tres dimensiones (piensa en una burbuja flotando en el espacio). La idea intuitiva es que la divergencia mide el flujo hacia afuera en puntos individuales, mientras que el flujo mide la cantidad de fluido que sale de toda una región. Así que al sumar todos los cachitos de divergencia se obtiene el mismo valor que el flujo.
Teorema de la divergencia en esféricas parte 2 YouTube

Sea F= x^3i + y^3j+z^3k. Evaluar la integral de superficie de F sobre la esfera unitaria.Más enunciados de problemas y sus soluciones en https://a2formacion..