Triangle Inequality Proof

Euclidean distance Engati

The triangle inequality is a defining property of norms and measures of distance. This property must be established as a theorem for any function proposed for such purposes for each particular space: for example, spaces such as the real numbers, Euclidean spaces, the L p spaces ( p ≥ 1 ), and inner product spaces .

linear algebra Explanation for the proof of Ptolemyinequality Mathematics Stack Exchange

then be too large, violating the reverse triangle inequality. m-defectiveness The second idea is to allow for a relaxed triangle inequality. We do so by deﬁning a distance measure to be m-defective w.r.t a given domain if there exists a ﬁxed m 1 such that for all triples of points x;y;z , we have that jD(x;y) D(x;z)j mD(y;z).

INH Triangles Triangle Inequality Theorem 3 YouTube

Lack of triangle inequality: Since the Bregman divergence is essentially a generalization of squared Euclidean distance, there is no triangle inequality.. , which may be positive or negative. Proofs. Non-negativity and positivity: use Jensen's inequality. Uniqueness up to affine difference: Fix some , then for any.

Triangle Inequality Mathematics Euclidean Geometry, PNG, 1280x998px, Triangle Inequality, Area

I'm looking to introduce my students to the triangle inequality in the plane with the regular euclidean distance. They have no knowledge of functions or vectors (and therefore norms) so the proof should contain no mention of those concepts. I'm finding it rather difficult to prove with such basic tools.

proof of CauchySchwarz inequality, proof of Triangle Inequality Calculus Coaches

Reverse Triangle Inequality Proof Metric Spaces YouTube

(N4) kx+ yk5kxk+ kyk, the triangle inequality. Proofs of (N1), (N2), and (N3) are elementary applications of the de nition of the norm. We brie y defer the proof of (N4), until we've de ned the dot product and proved the Cauchy-Schwarz Inequality. With a formal de nition of the length of vectors, we have an obvious way to de ne distance in Rn:

ShowMe triangle Inequality Theorem

Q: Why is it called the triangle inequality? A: Analogue with euclidean distance in the plane: picture Defn: Minimum Distance of a code C: d(C) = min(d(c;c0) : c;c02C;c 6=c0) Notation: (n;M;d)-code: a code of length n, size M and mini-mum distance d { The larger M is, the more distinct messages can be transmitted.

Triangle Inequality Property for the Euclidean Metric Mathematics Stack Exchange

The convergence problems mentioned in Example~B.4.3 leads to the common practice of defining the metric structure on $\R^{\infty}$ using the distance function $\bar d$ in Example B.4.4 rather than the Euclidean distance. In fact, whenever we refer to the metric structure of $\R^{\infty}$ we will assume the metric structure of $\bar d$ derived.

Example 20 Show a + b

Squared Euclidean distance does not form a metric space, as it does not satisfy the triangle inequality. However it is a smooth, strictly convex function of the two points, unlike the distance, which is non-smooth (near pairs of equal points) and convex but not strictly convex.

Indirect Proof and Inequalities in One Triangle YouTube

This is the continuous equivalent of the Euclidean metric in Rn. The proof of the triangle inequality follows the same form as in that case. 8. Sas in 7. d(f;g) = max a x b jf(x) g(x)j: This is the continuous equivalent of the sup metric. The proof of the triangle inequality is virtually identical.

Reverse Triangle Inequality Proof YouTube

Theorem. Let x,y x, y be vectors in the real Euclidean space Rn R n . Let ∥⋅∥ ‖ ⋅ ‖ denote vector length . Then: ∥x +y∥ ≤ ∥x∥ +∥y∥ ‖ x + y ‖ ≤ ‖ x ‖ + ‖ y ‖. If the two vectors are scalar multiples where said scalar is non-negative, an equality holds: ∃λ ∈R, λ ≥ 0: x = λy ∥x +y∥ = ∥x∥.

Triangle Inequality Simple Proof PeakD

a task. When deﬁning distances, the triangle inequality has proven to be a useful constraint, both theoretically—to prove convergence and optimality guarantees— and empirically—as an inductive bias. Deep metric learning architectures that respect the triangle inequality rely, almost exclusively, on Euclidean distance in the latent space.

[Solved] Proof of triangle inequality 9to5Science

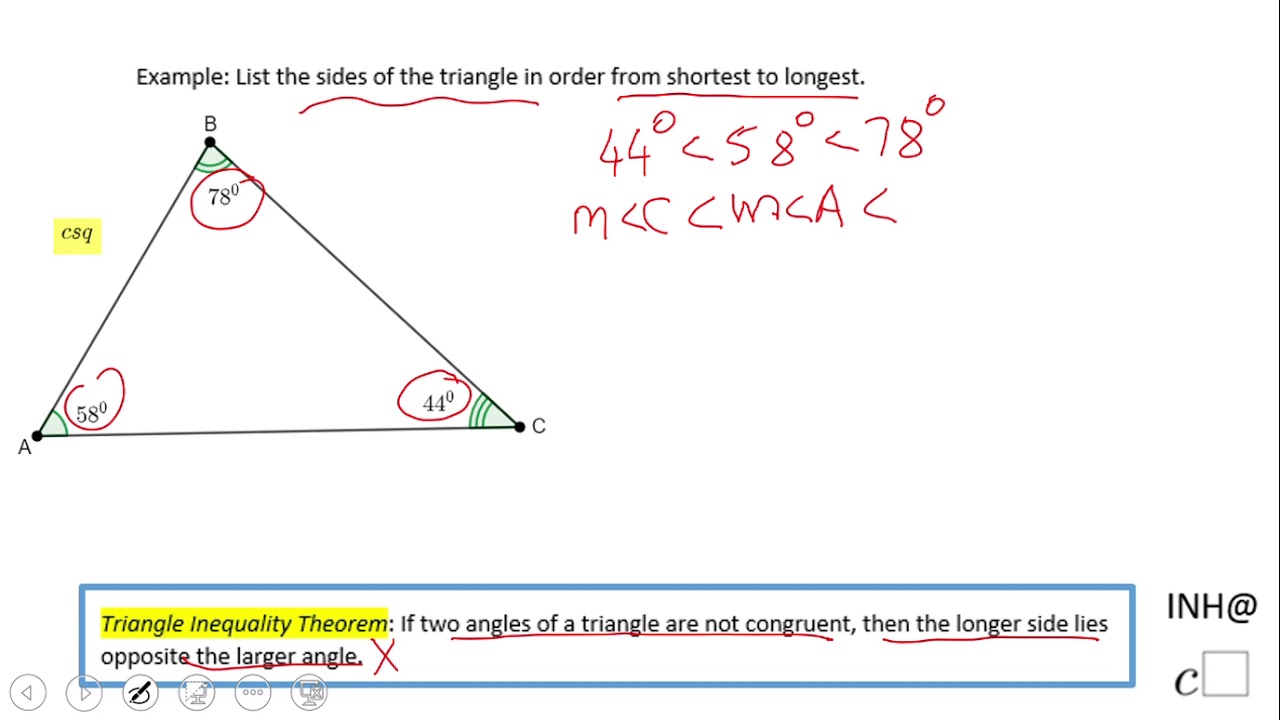
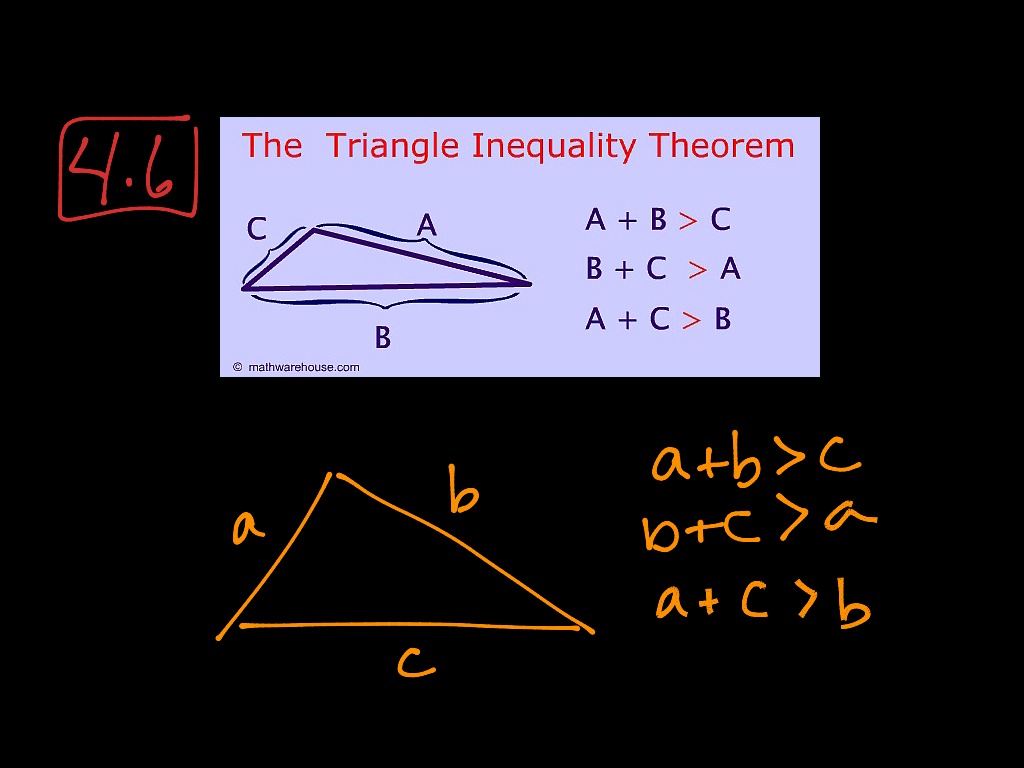
Triangle Inequality Theorem

The formula for Euclidean distance in two dimensions is D = ( x 2 − x 1) 2 + ( y 2 − y 1) 2, where D is the Euclidean distance, and ( x 1, y 1) and ( x 2, y 2) are the Cartesian coordinates of.

geometry Euler triangle inequality proof without words Mathematics Stack Exchange

In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance.These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not.

[Solved] Proof for triangle inequality for vectors 9to5Science

Then d is a metric on R2, called the Euclidean, or ℓ2, metric. It corresponds to the usual notion of distance between points in the plane. The triangle inequality is geometrically obvious, but requires an analytical proof (see Section 7.6). Example 7.5. The Euclidean metric d: Rn ×Rn → R on Rn is deﬁned by d(x,y) = √ (x1 −y1)2 +(x2.